データの正規性とは、データが正規分布しているかどうかのこと。
正規分布を前提にした統計手法が多いため、データが正規分布をしているかどうかが問題になることが多い。
正規分布かどうかの検定
データが正規分布しているかどうかの検定には、Shapiro-Wilk test (シャピロ・ウィルクの検定)がある。
帰無仮説は「正規分布している」なので、棄却されないほうがいい。
帰無仮説が棄却されないときは、統計学的な結論ではないので、正規分布を積極的に証明しているわけではないことに注意。
> shapiro.test(sleep$extra) Shapiro-Wilk normality test data: sleep$extra W = 0.94607, p-value = 0.3114
このデータの場合は、正規分布していると考えてよい。
ヒストグラムを見てみると、悪くはない。
hist(sleep$extra)
サンプルサイズを見てみると、20例。
> length(sleep$extra) [1] 20
グループごとの正規分布の検定
グループごとにShapiro-Wilk検定を行うにはどうするか?tapply()という関数を使う。
sleepというデータフレームには、groupという変数があり、groupは1と2がある。
group別にextraというデータが正規分布しているかどうかを見る。
> tapply(sleep$extra,sleep$group,shapiro.test) $`1` Shapiro-Wilk normality test data: X[[i]] W = 0.92581, p-value = 0.4079 $`2` Shapiro-Wilk normality test data: X[[i]] W = 0.9193, p-value = 0.3511
Shapiro-Wilk test の帰無仮説は、正規分布している、なので、棄却されなかったから、上記の2グループともに、正規分布してそう、という結果。
グラフを左右に並べたいときは、グラフウィンドを横長にしてから、layout(t(1:2))を実行する。
そのあとにtapply()でグループごとのグラフを描く。
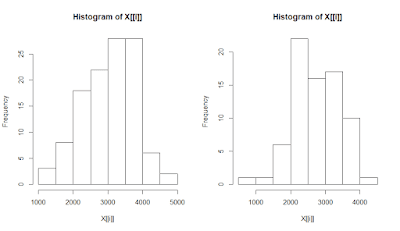
layout(t(1:2)) tapply(sleep$extra, sleep$group, hist)
左がgroup1、右がgroup2。
正規性の確認もう一つの例
MASSパッケージのbirthwtデータフレームを使う。
smoke(母親の喫煙)別のbwt(出生時体重)比較をする。
MASSパッケージを呼び出して、bwtのヒストグラムを描く。
正規分布しているように見える。サンプルサイズは189。
library(MASS) hist(birthwt$bwt)
喫煙か非喫煙かでグラフを描く。
左がsmoke=0で非喫煙、右がsmoke=1で喫煙。
layout(t(1:2)) with(birthwt, tapply(bwt, smoke, hist))
正規性の確認の方法としてQQプロットという方法がある。
横軸に理論的な分位数(クォンタイル)、縦軸に実際の値としてプロットする。対角線上にプロットが並べば、正規分布と考えられる。
with(birthwt, tapply(bwt, smoke, qqnorm))
まっすぐに並んでいるとはいいがたいが、まったくずれているとも言えないので、正規分布の範囲内と考えていい。
グループごとにShapiro-Wilk検定を実施すると、smoke=0もsmoke=1もどちらも有意でなく、正規分布と言ってよい。
> with(birthwt, tapply(bwt, smoke, shapiro.test)) $`0` Shapiro-Wilk normality test data: X[[i]] W = 0.98694, p-value = 0.3337 $`1` Shapiro-Wilk normality test data: X[[i]] W = 0.98296, p-value = 0.4195
平均と標準偏差も見ておくと、ともに平均は標準偏差の3倍以上。上か下のすそ野のが途中で切れていることもない。
> with(birthwt, tapply(bwt, smoke, mean)) 0 1 3055.696 2771.919 > with(birthwt, tapply(bwt, smoke, sd)) 0 1 752.6566 659.6349
最後に、グラフウィンドを閉じてlayout()をリセットしてから、四角いウィンドで箱ひげ図を描いてみる。飛び離れた値もなさそうなことがわかる。
boxplot(bwt ~ smoke)
まとめ
データ分析を進めるにあたり、データの正規性を確認する方法をまとめた。
最低限ヒストグラムは見てみる。余力があればQQプロットも描いてみる。Shapiro-Wilk検定もしてもいいが結果にとらわれないようにする。
以上がデータの正規性の確認だ。
編集後記「正規性を気にしすぎている」
個人的には多くの人が正規性を気にしすぎだと思う。
確かに、初学者だったころ、ぼくも非常に気になった。
しかし、データが正規分布していようがしてまいが、現実世界では正規分布を前提としたパラメトリックな手法が、ばんばん使われている。
教科書は教科書であって、研究発表の現場ではそこまで気にしていない。
結論としては、
- 自分がある程度納得できる範囲で確認する。
- 聞かれたら「チェックはしました」と言える程度に確認する。
- 対数変換などをしたほうが明らかに適切なら当然実施する。
という程度でよい。
そんなことよりも、比較対照がない観察研究で、多変量調整をしなければならない状況なのに、多変量調整をしないほうがよほど問題。
正規性にとらわれると統計手法の選択肢が非常に狭まる。
正規性は四角四面に考えないことだ。