線形混合モデルをSPSSで実行する方法の解説。
反復測定データで、欠損値があってもできる限りデータを使用できる点で、反復測定分散分析よりも適切な方法だ。
- 線形混合モデルをSPSSで実行するために使用するサンプルデータ
- 線形混合モデルの前に反復測定分散分析を行ってみる
- 線形混合モデルをSPSSで実施してみる
- 線形混合モデルをSPSSで実施した後の結果の読み方
- 線形混合モデルをSPSSで行う際に反復測定の時間の項を連続量で投入すると・・・
- 線形混合モデルをSPSSで実施する際に分散共分散を無構造にするとどうなるか?
- まとめ
- EZR公式マニュアル
- SPSSによる分散分析・混合モデル・多重比較の手順
線形混合モデルをSPSSで実行するために使用するサンプルデータ
EZR公式マニュアル付属のデータ FCZ_CSA.rda を用いる。
3群で3回の反復測定連続データである。
平均値と95%信頼区間のグラフを描くとこんな感じ。

推定周辺平均が計算されているので、単純な平均値ではないが、いわゆる平均値の折れ線グラフである。
線形混合モデルの前に反復測定分散分析を行ってみる
SPSSで反復測定分散分析を行うには、「分析」→「一般線型モデル」→「反復測定」を選択。

反復測定の因子の定義の設定方法は、過去記事参照。

被験者内効果の結果は以下の通りである。
球面性の仮定は置けない結果になっているので、Greenhouse-Geisserの行の結果を見ることになる。


被験者間効果の結果は、以下の通り。

線形混合モデルをSPSSで実施してみる
線形混合モデルは、被験者のばらつきを変量効果として考慮したモデルで、少しの欠測値があってもそのまま解析して問題ないところが利点。
サンプルデータは実際ちらほら欠測値がある。
赤矢印部分が欠測値。

まず、データを一人1行ではなく、全目的変数を一列に並べる作業を行う。
反復測定分散分析は、一人1行のデータにしていたが、それを縦に積み重ねる。
これはEZRで実施したほうが簡単なので、SPSSに移植してくる前に縦に積み重ねてから、SPSSに持ってきた。
CDratioという目的変数が縦方向に一列に並んでいる。
それが、被験者と時点が他の変数で区別されるようになっている。

ここまで準備が終わったら、いよいよ解析する。
「分析」→「混合モデル」→「線型」と選択すると、線形混合モデルが選択できる。
ちなみに、線型と線形は同じものを指しているので、漢字の違いは気にしない。

被験者に id(被験者ID)と FCZ(群別変数)、反復測定に反復測定を区別する変数 Weeks(カテゴリ変数の週数)を投入する。
反復測定共分散は、複合シンメトリ(Compound Symmetry)を選択する。
反復測定データの誤差の分散共分散が、どのような構造になっているかを指定する。
複合シンメトリはそろっていること(等分散・等共分散)を想定している。
あとで、そろっていない「無構造」もやってみる。
続行をクリックした後の窓で、従属変数にCDratio、因子にFCZとWeeksを投入する。

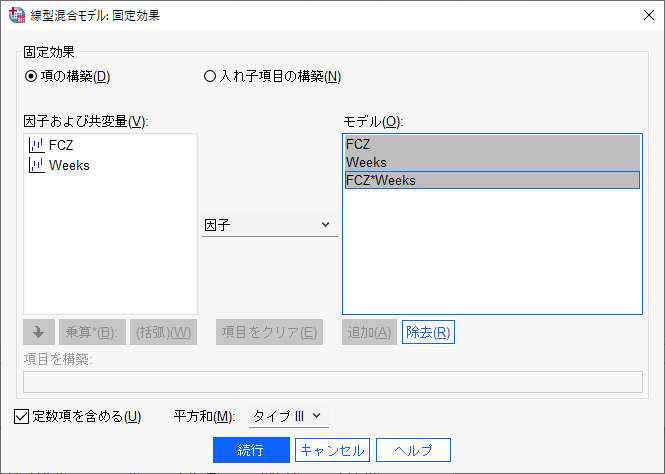
「固定」ボタンをクリックして、モデルを追加する。
左のFCZとWeeksを同時に選択して、追加をクリックすると、以下のようになる。
続行で戻る。
「統計量」ボタンをクリックして、固定効果のパラメータ推定値にチェックを入れる。
続行で戻る。

OKをクリックすると結果が出力される。
線形混合モデルをSPSSで実施した後の結果の読み方
固定効果のANOVA の結果は以下の通り。
反復測定分散分析とは少し異なるが、傾向は似ている。

固定効果の推定値は、以下の通り。
反復測定分散分析はこういう結果は出せないので、回帰分析グループの線形混合モデルならではの出力である。

欠測値の影響を受けにくく、欠測含め171例中、反復測定分散分析では163例が計算に使われたが、線形混合モデルでは170例が計算に使われていた。


線形混合モデルをSPSSで行う際に反復測定の時間の項を連続量で投入すると・・・
反復測定の時間を連続量で投入して、直線的に変化すると仮定するとどうなるか?
反復測定にWeeksNum(数値データ)を投入する。

因子のWeeksを戻し、共変量にWeeksNumを入れる

固定効果は、FCZとWeeksNumの主効果と交互作用をともに設定する。

固定効果の推定の結果は以下の通り。

線形混合モデルをSPSSで実施する際に分散共分散を無構造にするとどうなるか?
無構造というのは、特に想定なしということである。

固定効果の推定結果は、以下の通り。
複合シンメトリと少し異なるがほぼ同じ結果だ。

共分散パラメータの推定値は以下のようになる。

まとめ
線形混合モデルをSPSSで実施する方法を解説した。
欠測値が少々あっても計算に使ってくれるという点でよいモデルだ。
誤差の分散共分散構造は、複合シンメトリにしておけばよいだろう。
何の前提もなしとするなら、無構造がよいかもしれない。
反復測定データは、ぜひ線形混合モデルで解析することをおすすめしたい。



