回帰分析をする際に、説明変数や目的変数が正規分布をしていないことで悩んでいる人は多い。
悩むところはそこじゃない。
重回帰分析では、残差が正規分布している必要がある。
- 重回帰分析の前提は何か?
- 重回帰分析の残差の正規性はどうやって確認するか?
- 重回帰分析の残差の正規分布の確認はSPSSでどうやるか?
- 重回帰分析の説明変数や目的変数は正規分布していなくてもよいか?
- 重回帰分析の残差が正規分布していない場合はどうしたらよいか?
- まとめ
- 動画解説
- 参考図書
重回帰分析の前提は何か?
重回帰分析の前提は4つある。
- 独立性(データそれぞれが独立)
- 等分散性(説明変数にかかわらず分散が一定)
- 正規性(誤差自体が正規分布している)
- 線形性(説明変数と目的変数の関係は直線で近似できる)
1.独立性、2.等分散性、3.正規性の3つは、残差が満たす必要がある。
残差とは、目的変数の実際の値と、回帰式で計算された予測値の差を言う。
この残差を、誤差の代わりに使っている。
誤差は、目的変数の実際の値と、真の回帰式で計算される目的変数の真の値の差。
真の値は測定できず推測しかできないため、真の誤差は計算できない。
それゆえ、残差を使うわけである。
残差プロットに特異なパターンがなければ、1.独立性は満たされる。
残差が均一ならば、2.等分散性の仮定は満たされる。
では、正規性はどうやったら確認できるか?
重回帰分析の残差の正規性はどうやって確認するか?
重回帰分析の結果から残差を計算しQQ plotを描く。残差のプロットが直線状に乗っている場合は、正規分布していると見ていい。
例1
ISLR パッケージの Auto データを使った例。ISLR パッケージはインストールが必要なパッケージだ。
install.packages("ISLR")
library()でISLR パッケージを呼び出した後、Autoを少し加工して、交互作用項を含めた重回帰モデルでmpg (mile per gallon) つまり燃費を予測する回帰式を作る。
library(ISLR) Auto1 <- Auto[1:8] res2 <- lm(mpg ~ cylinders + displacement + horsepower + weight + acceleration + year + year:displacement + factor(origin), data=Auto1) layout(t(matrix(c(1:4),nr=2))) plot(res2)
回帰診断のためのプロットは以下の4つが出力される。右上がQQ plotだ。プロットした丸が直線状にきれいに乗っていれば、残差が正規分布していると言える。右上端が少し外れているが、おおむね直線状に乗っていると言える。つまり、残差は正規分布していると言える。

例2
ISLR パッケージの Carseats データセットを使った例でも確認してみる。
result2 <- lm(Sales ~ Price + factor(ShelveLoc) + factor(US), data=Carseats) layout(t(matrix(c(1:4),nr=2))) plot(result2)
右上のQQ plotでは、おおむね直線状にプロットされている。残差は正規分布していると言える。
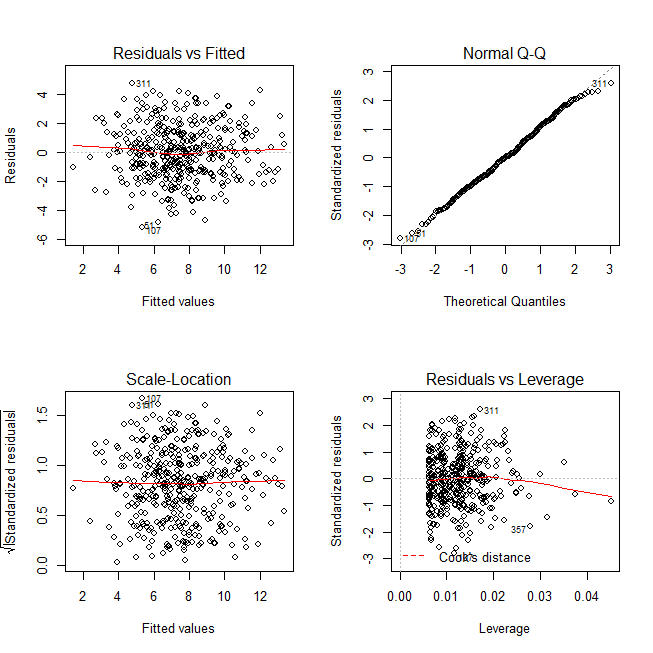
ちなみに例1、例2とも、回帰診断プロットの左上のFitted values vs. Residualsに一定の傾向がないことが大事。特異なパターンがなければ、独立性が確保されている。また、増大傾向や縮小傾向がなければ、等分散性も言える。
回帰診断によって、残差の正規性のみならず、独立性、等分散性が言えるわけである。
重回帰分析の残差の正規分布の確認はSPSSでどうやるか?
分析→回帰→線型と進み、ダイアログボックスの「作図」をクリックして、正規確率プロットにチェックをするとP-Pプロットが描かれる。

これは、上述のQ-Qプロットと同様のもので、Q-Qプロットが正規分布の理論的なクオンタイル(分位数)との比較だったのに対し、P-Pプロットは正規分布の理論的な累積確率と比較する。
いずれにしても、対角線上にプロットが乗るかどうかで検討する。

参考ウェブサイト
Q-QプロットとP-Pプロットの意味と違い - 具体例で学ぶ数学
重回帰分析の説明変数や目的変数は正規分布していなくてもよいか?
重回帰分析の説明変数や目的変数は正規分布していなくてもよいか?という質問に対しては、「していなくてよい」が答えだ。
正規分布している必要があるのは残差なのだ。説明変数や目的変数ではない。これを間違えてはいけない。
残差が正規分布している必要がある理由は、回帰モデルの有意性確認に使う分散分析の検定の検定統計量の分母に該当するから。
分布は、分母・分子とも正規分布していることが前提だからだ。
重回帰分析の残差が正規分布していない場合はどうしたらよいか?
残差が正規分布していない場合はどうしたらよいか?
実はここで初めて目的変数の分布が話題に上る。この順番でなければいけない。
目的変数が正規分布からかなりずれていた場合、正規分布になるように変換する方法を取るとうまくいくことがある。
一番多いのは自然対数変換だ。統計ソフトRならlog()という関数を使う。エクセルならln()だ。
自然対数変換をすると正規分布に近づく変数は多い。特に血液検査値など生命に関する測定値は自然対数変換が有効なことが多い。
自然対数変換して、正規分布に近づけた目的変数を使うと、残差も正規分布することが多い。
もしも、目的変数を正規分布に近づけても、残差が正規分布しないようであれば、(線形)回帰分析をあきらめるしかないかもしれない。
(線形)回帰分析をあきらめる場合は、目的変数を中央値などで2つに分け、ロジスティック回帰分析を行うなどの方法がある。
連続量を二値にしてしまうので、情報の損失があるので、モデルの適切性と天秤にかけ、どちらを取るか、慎重に吟味する必要がある。
まとめ
重回帰分析の説明変数や目的変数は正規分布していなくてもよいか?この問題に頭を悩ませている人は多い。
大事なのは、重回帰分析の残差が正規分布していることだ。それも検定で確認せよということではなく、図でだいたい正規分布していることをQ-QプロットやP-Pプロットで見ればよい。
正規性から大きく外れているなら、目的変数の分布をチェックして、正規分布から外れているようなら、対数変換などを試みよう。
目的変数の対数変換による正規分布化によって、解決することも多いだろう。
何らか参考になれば。
動画解説
参考図書
医学への統計学
EZR公式マニュアル
SPSSで学ぶ医療系多変量データ解析 第2版




