メタ解析のやり方　平均値の差のメタ解析

平均値の差のメタ解析のやり方を解説。

↑1万人以上の医療従事者が購読中

メタ解析のやり方解説のためのサンプルデータ
メタ解析のやり方のサンプルデータ　それぞれの試験の平均値の差と95%信頼区間
メタ解析のためにそれぞれの試験の平均値の差と95%信頼区間のグラフ化
メタ解析１　固定効果の計算
メタ解析２　変量効果の計算（DerSimonian-Lairdの方法）
メタ解析のグラフ　統合平均値と95%信頼区間を書き入れる
メタ解析の結果を出力する
メタ解析をより柔軟な変量モデル―制限付き最尤推定量（REML）で行う
メタ解析を metafor パッケージを使って行う方法
まとめ
引用書籍

メタ解析のやり方解説のためのサンプルデータ

メタ解析のやり方を解説するためのデータは以下の通り。

mが平均、sが標準偏差、nがサンプルサイズ。

n1 <- c(155,31,75,18,8,57,34,110,60)
m1 <- c(55.0,27.0,64.0,66.0,14.0,19.0,52.0,21.0,30.0)
s1 <- c(47.0,7.0,17.0,20.0,8.0,7.0,45.0,16.0,27.0)
n0 <- c(156,32,71,18,13,52,33,183,52)
m0 <- c(75.0,29.0,119.0,137.0,18.0,18.0,41.0,31.0,23.0)
s0 <- c(64.0,4.0,29.0,48.0,11.0,4.0,34.0,27.0,20.0)

並べてみると以下の通り。

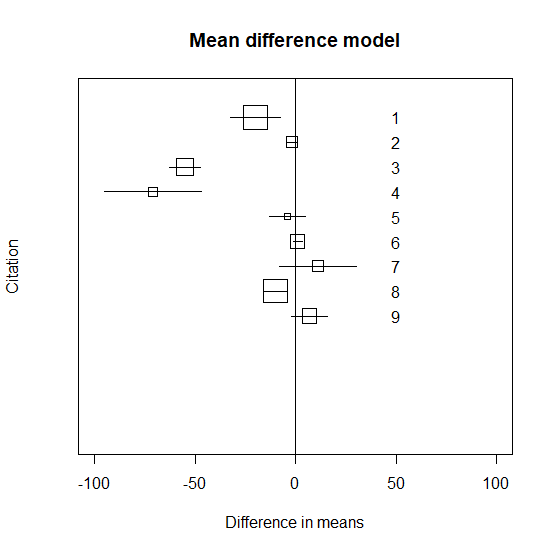
メタ解析のやり方のサンプルデータ　それぞれの試験の平均値の差と95%信頼区間

各試験の平均値の差を計算し、95％信頼区間を計算する。

# ---- difference in means -----

ad <- m1-m0
s <- ((n1-1)*s1^2+(n0-1)*s0^2)/(n1-1+n0-1)
se <- sqrt((1/n1+1/n0)*s)
tn <- n1+n0
low <- ad-1.96*se
upp <- ad+1.96*se

平均値の差と95％信頼区間の一覧を出力してみると、以下のようになる。

＞＞もう統計で悩むのを終わりにしませんか？

↑1万人以上の医療従事者が購読中

メタ解析のためにそれぞれの試験の平均値の差と95%信頼区間のグラフ化

各試験の平均値の差と95％信頼区間をグラフに書いてみる。

# ----- individual graph -----

k <- length(n1)
id <- k:1
plot(ad, id, ylim=c(-4,10), pch=" ", 
     xlim=c(-100,100), yaxt="n",
     ylab="Citation", xlab="Difference in means")
title(main=" Mean difference model ")
symbols(ad, id, squares=sqrt(tn), add=T, inches=0.25)
abline(v=0)
for (i in 1:k){
 j <- k-i+1
 x <- c(low[i], upp[i])
 y <- c(j, j)
 lines(x, y, type="l")
 text(50, i, j)
}

メタ解析１　固定効果の計算

固定効果とは、研究の結果が似ていると思えるときに使える方法。

メタ解析には、まず固定効果で統合する。

# ----- fixed effects -----

w <- 1/se/se
sw <- sum(w)
adm <- sum(ad*w)/sw
adl <- adm-1.96*sqrt(1/sw)
adu <- adm+1.96*sqrt(1/sw)
q1 <- sum(w*(ad-adm)^2)
df1 <- k-1
pval1 <- 1-pchisq(q1, df1)
q2 <- adm^2*sw
df2 <- 1
pval2 <- 1-pchisq(q2, df2)

統合平均値差、95％信頼区間下限、上限を並べてみると以下の通り。

均質性の検定、有意性の検定の各p値を並べてみると以下の通り。

統計学的有意であるが、均質性の検定に関しても有意、つまり異質性ありなので、変量効果で統合するほうがよさそうである。

メタ解析２　変量効果の計算（DerSimonian-Lairdの方法）

変量効果とは、研究同士に無視できない違い（異質性）があるときに使う方法。

# ----- random effects -----

tau2 <- (q1-(k-1))/(sw-sum(w*w)/sw)
tau2 <- max(0, tau2)
wx <- 1/(tau2+se*se)
swx <- sum(wx)
admx <- sum(ad*wx)/swx
adxl <- admx-1.96*sqrt(1/swx)
adxu <- admx+1.96*sqrt(1/swx)
qx2 <- admx^2*swx
pvalx2 <- 1-pchisq(qx2, df2)

変量効果による統合点推定値、95％信頼区間を表示すると以下のとおりである。

有意性の検定結果は以下のとおりである。

メタ解析のグラフ　統合平均値と95%信頼区間を書き入れる

先ほどのグラフに統合平均値と95%信頼区間を書き入れる。

# ----- graph -----

x <- c(adl, adu)
y <- c(-1, -1)
lines(x, y, type="b")
x <- c(adxl, adxu)
y <- c(-2, -2)
lines(x, y, type="b")
abline(v=c(adm, admx), lty=2)
text(60, -1, "Combined: fixed")
text(60, -2, "Combined: random")

メタ解析の結果を出力する

ここまで、途中途中で結果を出力してきたが、以下にまとめて出力する。

adFE, LL, ULは、固定効果の統合平均値と95%信頼区間、Q1, df1, p1は均質性の検定（検定統計量、自由度、P値）、Q2, df2, p2は有意性の検定（検定統計量、自由度、P値）である。

adDL, LL, ULは変量効果の統合平均値と95%信頼区間、Q2DL, df2, p2DL は変量効果の有意性の検定、tau2は ${\tau}^2$ の推定値である。

メタ解析をより柔軟な変量モデル―制限付き最尤推定量（REML）で行う

変量モデルのDerSimonian-Lairdの方法は簡便な方法だが、より柔軟で理論的に自然な方法が制限付き最尤推定量（REML, restricted maximum likelihood estimator）だ。

現代はPCを使って反復計算が簡単にできるようになったので、REMLの適用が望ましい。

Newton-Raphson法を用いて繰り返し収束計算で ${\tau}^2$ の推定値を求めている。

# ----- REML method -----

intau <- tau2
tau <- intau
#
nrep <- 10
newt <- 1:nrep
for (i in 1:nrep){
 wb <- 1/(tau+se*se)
 admb <- sum(ad*wb)/sum(wb)
 qf <- k/(k-1)*(ad-admb)^2-se*se
 dkx <- (-1*sum(ad*wb*wb)+admb*sum(wb*wb))/sum(wb)
 qf2 <- -2*k/(k-1)*(ad-admb)*dkx
 h <- sum(wb*wb*(qf-tau))
 dh <- sum(-2*wb*wb*wb*(qf-tau)+wb*wb*(qf2-1))
 newt[i] <- tau - h/dh
 rel <- abs((newt[i]-tau)/tau)
 tau <- newt[i]
}

# ----- 統合値の計算 有意性の検定 -----
wg <- 1/(tau+se*se)
swg <- sum(wg)
adRM <- sum(ad*wg)/swg
adRMl <- adRM-1.96*sqrt(1/swg)
adRMu <- adRM+1.96*sqrt(1/swg)
qx2RM <- adRM^2*swg
pvalx2RM <- 1-pchisq(qx2RM, df2)
tau2 <- tau

# ----- 統合値をグラフに書き入れる -----
x <- c(adRMl, adRMu)
y <- c(-3, -3)
lines(x, y, type="b")
abline(v=adRM, lty=2)
text(60, -3, "Combined: REML")

REMLの結果をグラフに足すと以下のようになる。

計算結果は、以下の通り。

DerSimonian-Lairdの方法よりもさらに95%信頼区間が広がっていて、統計学的有意でなくなっている。

メタ解析を metafor パッケージを使って行う方法

Rのmetafor パッケージを使うと簡単にメタ解析ができる。

インストールしたあと、library() で呼び出しておく。

install.packages("metafor") #1回のみ
library(metafor) #使うときに

計算は以下のように行う。

ポイントは、escalc()関数とrma.uni()関数である。

# データ再掲
n1 <- c(155,31,75,18,8,57,34,110,60)
m1 <- c(55.0,27.0,64.0,66.0,14.0,19.0,52.0,21.0,30.0)
s1 <- c(47.0,7.0,17.0,20.0,8.0,7.0,45.0,16.0,27.0)
n0 <- c(156,32,71,18,13,52,33,183,52)
m0 <- c(75.0,29.0,119.0,137.0,18.0,18.0,41.0,31.0,23.0)
s0 <- c(64.0,4.0,29.0,48.0,11.0,4.0,34.0,27.0,20.0)

# データフレームに変換
dat <- data.frame(m1, s1, n1, m0, s0, n0)

# 推定値と分散の計算
dat.escalc <- escalc(measure="MD", vtype="HO",
m1i=m1, sd1i=s1, n1i=n1,
m2i=m0, sd2i=s0, n2i=n0,
data=dat)

# 統合値の計算
res.reml <- rma.uni(yi, vi, method="REML", 
data=dat.escalc)

summary(res.reml)